Are there enough neutrons for a thermal breeder?
NOTE: This is not a discussion of any physical or proposed reactor, it is a discussion of possible theoretical limits and consequences of various geometrical fuel arrangements.The conventional wisdom is that there are not enough neutrons for a uranium-plutonium thermal reactor to be a breeder. This is based on the definition of a breeder reactor and the properties of thermal neutron interactions with U-235 and U-238. A breeder reactor is defined as one where as many fertile atoms (U-238) absorb a neutron and are converted to fissile atoms (Pu-239) as fissile atoms (U-235 or Pu-239) absorb a neutron and are no longer fissile. For each 7 thermal neutrons absorbed by U-235, about 6 cause fission and about 1 causes transmutation to U-236. Therefore about 1.17 thermal neutrons are absorbed in U-235 for for each thermal fission of U-235. To have a uranium-plutonium thermal breeder another 1.17 thermal neutrons must be absorbed in U-238 to convert it to fissile Pu-239 for a cost of 2.34 thermal neutrons per thermal fission of U-235. In any real reactor there are other neutron losses (neutrons which escape the reactor or are absorbed in the moderator, the reflector, the reactor hardware, or fission products in the fuel) so more than 2.34 neutrons per thermal fission of U-235 are required. Each thermal fission of U-235 emits around 2.435 neutrons, clearly not enough (2.435 - 2.34 = .095), end of discussion. HOWEVER, the emitted neutrons are not thermal neutrons, they are mostly fast neutrons but it is complicated to discuss the interactions of fast neutrons with U-235 and U-238 so they are usually ignored.
It is true that in conventional water cooled reactors such as BWR or PWR light water reactors or CANDU heavy water reactors which all use thin fuel rods the fast fission of U-238 is around 3% or less and does not have enough impact to have a breeder. This is only a question of geometry, if the fuel is in a fat fuel rod instead of a thin one then the average distance traveled by an emitted neutron before it went from the fuel rod into the moderator would be much greater and the probability that it would cause fast fission of U-238 would also be much greater. This is difficult to analyze analytically but easy to check with MCNP simulations.
MCNP simulations were performed on a simple theoretical reactor model with only two materials: fuel and moderator. The reactor core is a right hexagonal prism with sides 18 m by 18 m. It is embedded in a reflector which is filled with moderator and is a right hexagonal prism with sides 20 m by 20 m. The core is filled with moderator and a hexagonal array of fuel rods which are 2 cm shorter than the core height. The variables are the fuel rod diameter, the center to center spacing of the fuel rods (pitch), the U-235 concentration in the fuel rods, and the moderator material. The large size and thick reflector ensures that peripheral neutron loss is low.
Several cases are considered: .875 cm diameter fuel rods in light water moderator, .875 cm fuel rods in heavy water moderator, and 10, 20, 30, and 40 cm fuel rods in heavy water moderator. The figure below shows the model reactor in a case with large diameter fuel rods. In the cases with the small fuel rods the figure would only show a barely visible pattern of very small dots and lines.
For these theoretical reactors the core size and reflector thickness were set large so that the edge effects were minimized. Then for each of the cases the fuel rod diameter and the moderator material were set. An initial guess at the pitch (center to center spacing of the fuel rods) and the fuel enrichment were provided. The software was set to run with the provided values and then repeat with several different pitch values around the initial value. The pitch value which gave the highest keff was saved and the process repeated changing the fuel enrichment value until a value was found which gave a keff value near 1.00000. The process was repeated for each of the cases.
The MCNP simulations were run with tallies so the rates of the various neutron interactions with the fuel isotopes could be determined. The rates of interest are: fission of U-235, neutron absorption in U-235, fission of U-238, and neutron absorption in U-238. The rate of fissile material lost is the sum of the rates of fission of U-235 and neutron absorption in U-235. The rate of new fissile material created is just the rate of neutron absorption in U-238. The conversion ratio is the rate of new fissile material created divided by the rate of fissile material lost.
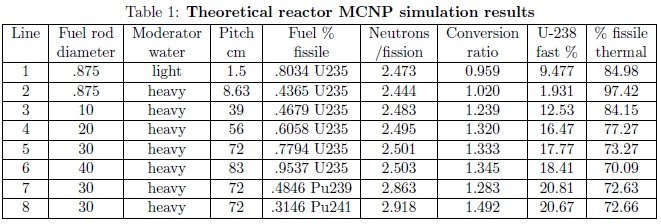
Table 1 shows the results of the simulations of the theoretical reactors at time zero. Since there is no structural material and no fission products in these reactors the results are better than can be achieved in any real reactor. They do provide some insight into the limits of what is achievable. In all cases the reactor is clearly a majority thermal reactor but also all have some fast fission of U-238. The sum of the last two columns is not 100% because there is some intermediate and fast fission of U-235. The light water case has a very small pitch and is consequently under moderated so there is a significant rate of fast fission of U-238. This provides support for the current interest in under moderated Light Water Reactors. In both cases with the small fuel rods (table lines 1 & 2) the theoretical maximum conversion ratio is too low to have a breeder, supporting the conventional wisdom. In the large tube cases (lines 3 to 6) the conversion ratio is greater than 1.23 and is large enough to suggest that a physical breed and burn reactor may be possible. The required concentration of U-235 to achieve criticality, the number of neutrons emitted per fission, and the conversion ratio all increase as the fuel rod diameter increases. The last two cases (lines 7 & 8), with Pu-239 and Pu-241 instead of U-235 as the fissile material are included to provide some insight to what might happen in an actual breed and burn reactor as the U-235 is gradually replaced with Pu-239 and eventually some Pu-241. The conversion ratio is not changed by much but the required fissile content is greatly reduced. In a breed and burn reactor like the proposed MUTBR most of the U-235 is consumed early in the long fuel life so later in the fuel life the fissile material is mostly plutonium isotopes.
For anyone interested in reproducing the results, the MCNP input file for each table line can be obtained with the links below.
MCNP inp file for table line 1
MCNP inp file for table line 2
MCNP inp file for table line 3
MCNP inp file for table line 4
MCNP inp file for table line 5
MCNP inp file for table line 6
MCNP inp file for table line 7
MCNP inp file for table line 8
page last modified 04/06/2022